第二百五十七章 见证奇迹吧!(上)
确定了,如果再求 加速度....”
加速度....”
听到基尔霍夫这番话。
原本就不怎么喧闹的教室,忽然又静上了几分。
对啊。
不知不觉中,徐云已经推导 了合外力和质量!
了合外力和质量!
如果再推导 加速度......
加速度......
那么不就可以以 二的形式,表达
二的形式,表达 波在经典
波在经典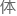 系
系 的方程了吗?
的方程了吗?
想到这里。
几位大佬纷纷拿 纸笔,尝试
纸笔,尝试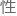 的计算起了最后的加速度。
的计算起了最后的加速度。
说起加速度,首先就要说说它的概念:
这个是用来衡量速度变化快慢的量。
加速度嘛,肯定是速度加得越快,加速度的值就越大。
比如我们经常可以听到的“我要加速啦”等等。
假如一辆车第1秒的速度是2m/s,第2秒的速度是4m/s。
那么它的加速度就是用速度的差(4-2=2)除以时间差(2-1=1),结果就是2m/s2。
再来回想一 ,一辆车的速度是怎么求
,一辆车的速度是怎么求 来的?
来的?
当然是用距离的差来除以时间差得 的数值。
的数值。
比如一辆车第1秒钟距离起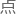 20米,第2秒钟距离起
20米,第2秒钟距离起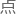 50米。
50米。
那么它的速度就是用距离的差(50-20=30)除以时间差(2-1=1),结果就是30m/s。
不知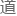 大家从这两个例
大家从这两个例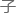 里发现了什么没有?
里发现了什么没有?
没错!
用距离的差除以时间差就得到了速度,再用速度的差除以时间差就得到了加速度,这两个过程都是除以时间差。
那么......
如果把这两个过程合到一块呢?
那是不是就可以说:
距离的差除以一次时间差,再除以一次时间差就可以得到加速度?
当然了。
这只是一种思路,严格意义上来说,这样表述并不是很准确,但是可以很方便的让大家理解这个思想。
如果把距离看作关于时间的函数,那么对这个函数求一次导数:
就是上面的距离差除以时间差,只不过趋于无穷小,就得到了速度的函数、
对速度的函数再求一次导数,就得到了加速度的表示。
鲜为人同学们懂不懂不知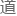 ,反正在场的这些大佬们很快便都想到了这一
,反正在场的这些大佬们很快便都想到了这一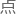 。
。
是的。
之前所列的函数f(x,t)描述的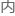 容,就是波段上某一
容,就是波段上某一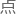 在不同时间t的位置!
在不同时间t的位置!
所以只要对对f(x,t)求两次关于时间的导数,自然就得到了这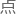 的加速度a。
的加速度a。
因为函数f是关于x和t两个变量的函数,所以只能对时间的偏导?f/?t,再求一次偏导数就加个2上去。
因此很快。
包括法拉第在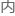 ,所有大佬们都先后写
,所有大佬们都先后写 了一个数值:
了一个数值:
加速度a=?2f/?t2。
而将这个数值与之前的合力与质量相结合,那么一个新的表达式便 现了:
现了:
f=t·sin(θ Δθ)-t·sinθ=μ·Δx?2f/?t2。
随后威廉·韦伯认真看了 这个表达式,眉
这个表达式,眉 微微皱了些许:
微微皱了些许:
“罗峰同学,这就是最终的表达式吗?我似乎 觉好像还能化简?”
觉好像还能化简?”
徐云 了
了
 :
:
“当然可以。”
f=t·sin(θ Δθ)-t·sinθ=μ·Δxa?2f/?t2。
这是一个最原始的方程组, 容不太清晰,方程左边的东西看着太麻烦了。
容不太清晰,方程左边的东西看着太麻烦了。
因此还需要对它 行一番改造。
行一番改造。
至于改造的思路在哪儿呢?
当然是sinθ了。
只见徐云拿起笔,在纸上画了个直角三角形。
众所周知。
正弦值sinθ等于对边c除以斜边a,正切值tanθ等于对边c除以邻边b。
徐云又画了个夹角很小的直角三角形,角度估摸着只有几度:
“但是一旦角度θ非常非常小,那么邻边b和斜边a就快要重合了。”
“这时候我们是可以近似的认为a和b是相等的,也就是a≈b。”
随后在纸上写到:
【于是就有c/b≈c/a,即tanθ≈sinθ。】
【之前的公式可写成f=t·tan
【1】【2】【3】【4】【5】
『加入书签,方便阅读』


