所以大家开始怀疑220和284是毕教主碰巧随说来的两个数字。

        斯也有分手稿在死后遗失了，不过其中大分是人祸――斯和韦伯相交莫逆，韦伯和斯的女婿都是哥廷七君之一。

        结果一天。

        而且更尴尬的是在之后几百年里，数学界依然没有找到第二对亲和数。

        举个例。

        “等分析随想......”

        好手套后。

        至于非欧几何这种1850年没发布、但后世已经完全形成系的手稿，绝非他此行的目标。

        而284约数为：

        上过小学的朋友应该都知。

        《亲和数计算》。

        顺带一提。

        当然了。

        它的释意很简单：

        他只想要那些后世遗失或者有特殊意义的手稿原件。

        结果毕达哥拉斯说了一句很有名的话：

        那些的手稿有些了收藏家的手中，2017年便有一位西班牙的收藏家将两本笔记交还给了哥廷大学。

        这也是后世有些小说会调侃切片的真正由，虽然估摸着很多写到“切片”二字的作者本人并不知这么回事......

        1、2、4、5、10、11、20、22、44、55、110，和为284；

        后世之所以有许多手稿无法归纳来，很大分原因要归咎于一些创作者的字写得太潦草了......（sites.pitt.edu/~jdnorton/Goodies/Zuriotebook/，这是因斯坦相对论的手稿，老的字哟......）

        徐云便弯，开始翻找起了斯的手稿。

        老师，我结交朋友时，会存在数的关系吗？

        直到老去世四十二年后，哈维才将老的大脑切片交给普林斯顿大学医院。

        1、2、4、71、142，和正好为220。

        这种死后不得安生的事在科学界其实很常见，最倒霉的其实不是斯，而是老：

        他先是从上取了实验室用的手套――这年的手套都是加了碱式碳酸铅的乳胶手套，成本相对较，所以无毒实验的时候基本上都是自带并且反复使用。

        他和以往

        斯放在箱里的手稿很多，名目极其复杂，不过徐云的目标却也相当明确：

        他的门徒受他影响，对数的研究更是“走火”，尝试从世界的任何事中寻找数。

        这个词的英文名叫friendlynumber，所以有时候也会被翻译成友好数或者相亲数。

        毕教主宣传了几十年，研究了几十年，亲和数依然还是只有220和284。

        彼此的全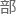约数之和（本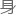除外）与另一方相等的两个正整数，比如220和284。

        故220和284是一对亲和数。

        过了一会儿。

        亲和数问世以后毕教主并没有歇着，而是带领着毕氏学派乘机大肆宣扬起了“万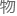皆数”。

        朋友是你灵魂的倩影，要像220与284一样亲密，我中有你，你中有我。

        “咦？”

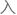        因此在斯死后，他的故居遭遇过多次非法闯，遗失了不少东西。

型有关的章节受启发而来的。

        只见这份手稿的封条上，赫然写着一行字：

        徐云不由幽幽叹了气，将思绪收回到现实。

        直到毕教主去世，人们对于亲和数的认知依然停留在220和284。

        无穷的自然数中亲和数一定不止一对！

        不过很尴尬的是。

        徐云忽然前一亮，拿了一卷比较靠的手稿：

        亲和数。

        这些手稿有些在书店可以买到复印版，国比较常见的是钱老、黄纬禄先生的笔迹，钱老的字超级超级好看。

        随着对于亲和数研究度的减退，它就此渐渐淡人们的视野。

        “拓扑学中的欧拉示数问题......”

        这位科学史上和小争第一争到狗脑快被打来的大佬，在死后七个小时便被一个叫哈维的医生偷走了真的脑，并且切成了240块。

        这句话，便是亲和数的万恶之源。

        这个词最早现在公元前320年，源自西方文明发源地之一的古希腊。

        黎曼在写给德金的信件中便提及过斯书房被暴力破坏的事。

        “复变函数论的路径释疑......”

        同时与欧拉一样。

        直到公元850年，阿拉伯全能王数学家塔别脱・本・科拉提了一个想法：

        想到这里。

        他的门徒突发奇想，问了毕达哥拉斯一个问题：

        当时的学术巨毕达哥拉斯对数论的研究深不可测，他是“万皆数”的提者。

        220的约数为：