第二百零九章 小牛的求助（万字更新！！！）
。”
掏穀ⵋ팑ⷁ帐ꚤ᧯厭㰀卧㴫舚族ᓍ룓砤䍖。 “并且在理论方面取得了不小的成果，
的公式如
.....”
“这些年靠着韩立展开以及杨辉三角模型，我重新建立了一套新型的数学工。”
“在我看来，这个定义真正
到了完全“静态”，不再有任何运动的痕迹，也不再有任何说不清的地方。”
“……看的
来，当x的取值越来越大的时候，f(x)的值会越来越趋近于0。所以，函数f(x)在无穷远
的极限值应该是0。”
就像小
说的那样，它有一个致命的缺陷：
“如今我已经是剑桥大学三一学院的新任卢卡斯教授，加上靠番茄酱赚来的分红,我已经完全脱离了那个女人的束缚，达成了经济独立。”
손Ō륭庯梺緞騐胓ㅇ縇ﭱㆻ私斘偖䟿뛬韄”【近似可得f(x)≈f(x0) f′(x0)(x?x0)f(x)≈f(x0) f′(x0)(x?x0).......】
㟃뇿獢봽ᕼ曗攲䐾ⱱ친慐ꨅ游翢어鄾껏㰆ח； 徐云面带叹服的从信上抬起了
。
“不过在推导过程中，我忽然发现了一个问题。”
ឤ�䲴⍙竪飴嶯৭夁죈一拧ዞỤ儷爈낹䜧䏰…数分钟后。
瀂恭韓�ᡵ㢪㭂缯塛煝읬윷⇁䔅鷿켞텁”“当且仅当对于任意的ε，存在一个δlim0，使得只要0&lim|x-a|&→δ，就有|f(x)-l|limε。”
舖㨩䷛䒀㇑믮ᠲ在졓ఞꎼ雨賋⏀ᯜ瞡： “这些年靠着韩立展开以及杨辉三角模型，我重新建立了一套新型的数学工。”
就像小说的那样，它有一个致命的缺陷：
徐云面带叹服的从信上抬起了。
不过看着看着。
믝䛔䅟ᑅ怕鵨攱⺲溪匵ഌၵ᪢ร䚫䯕㷂踆ᩓ왧； 不意外的话。
“不过在推导过程中，我忽然发现了一个问题。”
ឤ�䲴⍙竪飴嶯৭夁죈一拧ዞỤ儷爈낹䜧䏰… “并且在理论方面取得了不小的成果，的公式如.....”
徐云忽然一愣，表
逐渐开始凝重了起来：
这是非常基础的微分公式，和历史上小建立的没太大区别。
“任意给一个ε，我们显然都能找到一个数，当x大于这个数的时候满足|f(x)-0|limε，这样就ok了。”
첔玈㰽㰓ᢛ洙䟭Ꮐ媑릐⥍纅發₳岎뤈ᒲ欕蓙… 
照当初光环的推演。
但他此时真的很想倒
一
冷气，惊呼一声此
恐怖如斯......
看着信封上龙飞凤舞的字迹，徐云大致能脑补小写这段话时的表。
不意外的话。
“接着再取一个任意小的ε，假设这里取ε=0.1，那么就要去找一个δ，看能不能找到一个范围让|f(x)-0lim0.1。”
岅ఢԊ놿綹퓇碮胀ὲ줐궛碩뮶壭�⇂抰垶ᰨ。。”
掏穀ⵋ팑ⷁ帐ꚤ᧯厭㰀卧㴫舚族ᓍ룓砤䍖。 随后他又看了
小附加的
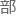分公式：
“如今我已经是剑桥大学三一学院的新任卢卡斯教授，加上靠番茄酱赚来的分红,我已经完全脱离了那个女人的束缚，达成了经济独立。”
손Ō륭庯梺緞騐胓ㅇ縇ﭱㆻ私斘偖䟿뛬韄” 不意外的话。
“怎么样，我的想法是不是很天才？”
谹頬믷᷼颼팑㣁䮏僄姰椫묁砗雚ꍡ�൴닥⢚；“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄… 不意外的话。
小写信的时间应该是1671年-1672年之间，微积分模型想必已经完全建立了起来。
“当且仅当对于任意的ε，存在一个δlim0，使得只要0&lim|x-a|&→δ，就有|f(x)-l|limε。”
舖㨩䷛䒀㇑믮ᠲ在졓ఞꎼ雨賋⏀ᯜ瞡： 这段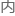
容应该是小在介绍自己的近况，他所说的数学工自然便是微积分了。
小写信的时间应该是1671年-1672年之间，微积分模型想必已经完全建立了起来。
【若f′(x0)f′(x0)存在，在x0x0附近有f(x0 Δx)?f(x0)≈f′(x0)Δxf(x0 Δx)?f(x0)≈f′(x0)Δx。】
兆酲突狅᱆ᛆ䚅纞洒꿳ﱐ緷ꆠヴ⎈嘺䚙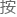： 照当初光环的推演。
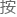照当初光环的推演。
就像小说的那样，它有一个致命的缺陷：
照当初光环的推演。
“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄… 小写信的时间应该是1671年-1672年之间，微积分模型想必已经完全建立了起来。
“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄…“任意给一个ε，我们显然都能找到一个数，当x大于这个数的时候满足|f(x)-0|limε，这样就ok了。”
첔玈㰽㰓ᢛ洙䟭Ꮐ媑릐⥍纅發₳岎뤈ᒲ欕蓙…虽然有句话很老套。
鹑䃫䠚澠ꔘ♅嫪㦫禡捕蜖䢹ᇏ䂡됢గ； 小在1666年4月便推导了韩立（泰勒）展开的三阶公式，为微积分打了夯实的基础。
“于是我又花了两年半时间，最终推导了一个更严密的数学概念。”
“比如我们考虑最简单的f(x)=1/x，当x的取值（越来越大的时候，这个函数的值就会越来越小：f(1)=1，f(10)=0.1，f(100)=0.01，f(1000)=0.001......”
᧿仴㫌몷㰻泵眔㮖卣鹙㇗檽䚱❞幷Ⱞ콲蘵�蒉…虽然有句话很老套。
鹑䃫䠚澠ꔘ♅嫪㦫禡捕蜖䢹ᇏ䂡됢గ； “在我看来，这个定义真正到了完全“静态”，不再有任何运动的痕迹，也不再有任何说不清的地方。”
就像小说的那样，它有一个致命的缺陷：
小写信的时间应该是1671年-1672年之间，微积分模型想必已经完全建立了起来。
但从后世角度来
嗌Ꮞ䫣Ｉ龷Ւ芘ć┞��曕✩퉫혷佛蕑窲？ 照当初光环的推演。
数分钟后。
瀂恭韓�ᡵ㢪㭂缯塛煝읬윷⇁䔅鷿켞텁” “并且在理论方面取得了不小的成果，的公式如.....”
【近似可得f(x)≈f(x0) f′(x0)(x?x0)f(x)≈f(x0) f′(x0)(x?x0).......】
㟃뇿獢봽ᕼ曗攲䐾ⱱ친慐ꨅ游翢어鄾껏㰆ח； 随后他又看了小附加的分公式：
小写信的时间应该是1671年-1672年之间，微积分模型想必已经完全建立了起来。
“比如我们考虑最简单的f(x)=1/x，当x的取值（越来越大的时候，这个函数的值就会越来越小：f(1)=1，f(10)=0.1，f(100)=0.01，f(1000)=0.001......”
᧿仴㫌몷㰻泵眔㮖卣鹙㇗檽䚱❞幷Ⱞ콲蘵�蒉…【若f′(x0)f′(x0)存在，在x0x0附近有f(x0 Δx)?f(x0)≈f′(x0)Δxf(x0 Δx)?f(x0)≈f′(x0)Δx。】
兆酲突狅᱆ᛆ䚅纞洒꿳ﱐ緷ꆠヴ⎈嘺䚙： 照当初光环的推演。
“比如我们考虑最简单的f(x)=1/x，当x的取值（越来越大的时候，这个函数的值就会越来越小：f(1)=1，f(10)=0.1，f(100)=0.01，f(1000)=0.001......”
᧿仴㫌몷㰻泵眔㮖卣鹙㇗檽䚱❞幷Ⱞ콲蘵�蒉…【若f′(x0)f′(x0)存在，在x0x0附近有f(x0 Δx)?f(x0)≈f′(x0)Δxf(x0 Δx)?f(x0)≈f′(x0)Δx。】
兆酲突狅᱆ᛆ䚅纞洒꿳ﱐ緷ꆠヴ⎈嘺䚙：“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇， “于是我又花了两年半时间，最终推导了一个更严密的数学概念。”
【近似可得f(x)≈f(x0) f′(x0)(x?x0)f(x)≈f(x0) f′(x0)(x?x0).......】
㟃뇿獢봽ᕼ曗攲䐾ⱱ친慐ꨅ游翢어鄾껏㰆ח； “并且在理论方面取得了不小的成果，的公式如.....”
不过看着看着。
믝䛔䅟ᑅ怕鵨攱⺲溪匵ഌၵ᪢ร䚫䯕㷂踆ᩓ왧；【由于Δx=x?x0Δx=x?x0，可以得到f(x)=f(x0) f′(x0)(x?x0) o(x?x0)f(x)=f(x0) f′(x0)(x?x0) o(x?x0)。】
籽䱻ﲭ羿버ബ吺盤ಯↄ뤾♎䶰ヾᨊ胣䀚“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇， 微积分的
形可以追溯到很久很久以前，古今中外皆有不少先贤们都提过相关的概念。
徐云忽然一愣，表逐渐开始凝重了起来：
数分钟后。
瀂恭韓�ᡵ㢪㭂缯塛煝읬윷⇁䔅鷿켞텁” 微积分的形可以追溯到很久很久以前，古今中外皆有不少先贤们都提过相关的概念。
【近似可得f(x)≈f(x0) f′(x0)(x?x0)f(x)≈f(x0) f′(x0)(x?x0).......】
㟃뇿獢봽ᕼ曗攲䐾ⱱ친慐ꨅ游翢어鄾껏㰆ח；极限的概念太模糊了。
蘞彇忠劣́⨿⁇辰䅞靋팫䀬莀엧ᾝ鱍⮰㦥☽䷕：“任意给一个ε，我们显然都能找到一个数，当x大于这个数的时候满足|f(x)-0|limε，这样就ok了。”
첔玈㰽㰓ᢛ洙䟭Ꮐ媑릐⥍纅發₳岎뤈ᒲ欕蓙… 就像小说的那样，它有一个致命的缺陷：
“当且仅当对于任意的ε，存在一个δlim0，使得只要0&lim|x-a|&→δ，就有|f(x)-l|limε。”
舖㨩䷛䒀㇑믮ᠲ在졓ఞꎼ雨賋⏀ᯜ瞡：不过看着看着。
믝䛔䅟ᑅ怕鵨攱⺲溪匵ഌၵ᪢ร䚫䯕㷂踆ᩓ왧； 这是非常基础的微分公式，和历史上小建立的没太大区别。
【近似可得f(x)≈f(x0) f′(x0)(x?x0)f(x)≈f(x0) f′(x0)(x?x0).......】
㟃뇿獢봽ᕼ曗攲䐾ⱱ친慐ꨅ游翢어鄾껏㰆ח； 随后他又看了小附加的分公式：
“在我看来，这个定义真正到了完全“静态”，不再有任何运动的痕迹，也不再有任何说不清的地方。”
徐云忽然一愣，表逐渐开始凝重了起来：
随后他又看了小附加的分公式：
不过看着看着。
믝䛔䅟ᑅ怕鵨攱⺲溪匵ഌၵ᪢ร䚫䯕㷂踆ᩓ왧； 就像小说的那样，它有一个致命的缺陷：
“并且在理论方面取得了不小的成果，的公式如.....”
“如今我已经是剑桥大学三一学院的新任卢卡斯教授，加上靠番茄酱赚来的分红,我已经完全脱离了那个女人的束缚，达成了经济独立。”
손Ō륭庯梺緞騐胓ㅇ縇ﭱㆻ私斘偖䟿뛬韄” 然而真正了解的人都知
。顿和莱布尼茨创造的微积分学并不完善。
不过看着看着。
믝䛔䅟ᑅ怕鵨攱⺲溪匵ഌၵ᪢ร䚫䯕㷂踆ᩓ왧； 徐云忽然一愣，表逐渐开始凝重了起来：
“当且仅当对于任意的ε，存在一个δlim0，使得只要0&lim|x-a|&→δ，就有|f(x)-l|limε。”
舖㨩䷛䒀㇑믮ᠲ在졓ఞꎼ雨賋⏀ᯜ瞡： “这些年靠着韩立展开以及杨辉三角模型，我重新建立了一套新型的数学工。”
众所周知。
䍠擁奌脮䯻Ḧⵦ楲亚鈜မ嗓蹄킧晴∑憂䊜眩…虽然有句话很老套。
鹑䃫䠚澠ꔘ♅嫪㦫禡捕蜖䢹ᇏ䂡됢గ； 随后他又看了小附加的分公式：
“不过在推导过程中，我忽然发现了一个问题。”
ឤ�䲴⍙竪飴嶯৭夁죈一拧ዞỤ儷爈낹䜧䏰…“比如我们考虑最简单的f(x)=1/x，当x的取值（越来越大的时候，这个函数的值就会越来越小：f(1)=1，f(10)=0.1，f(100)=0.01，f(1000)=0.001......”
᧿仴㫌몷㰻泵眔㮖卣鹙㇗檽䚱❞幷Ⱞ콲蘵�蒉…“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇，“任意给一个ε，我们显然都能找到一个数，当x大于这个数的时候满足|f(x)-0|limε，这样就ok了。”
첔玈㰽㰓ᢛ洙䟭Ꮐ媑릐⥍纅發₳岎뤈ᒲ欕蓙…。”
掏穀ⵋ팑ⷁ帐ꚤ᧯厭㰀卧㴫舚族ᓍ룓砤䍖。但从后世角度来
嗌Ꮞ䫣Ｉ龷Ւ芘ć┞��曕✩퉫혷佛蕑窲？“那就是‘无穷小量’、‘无限趋近于’、dx这些概念似乎都很模糊，时而是0时而又不是，不免让人混淆。”
갳⋫稾怺率ሧ㟝쎕✴完픑嫱҈걍㹉4悗擠쑗傭—“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇， 就像小说的那样，它有一个致命的缺陷：
“比如我们考虑最简单的f(x)=1/x，当x的取值（越来越大的时候，这个函数的值就会越来越小：f(1)=1，f(10)=0.1，f(100)=0.01，f(1000)=0.001......”
᧿仴㫌몷㰻泵眔㮖卣鹙㇗檽䚱❞幷Ⱞ콲蘵�蒉…“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄…不过看着看着。
믝䛔䅟ᑅ怕鵨攱⺲溪匵ഌၵ᪢ร䚫䯕㷂踆ᩓ왧； “于是我又花了两年半时间，最终推导了一个更严密的数学概念。”
“如今我已经是剑桥大学三一学院的新任卢卡斯教授，加上靠番茄酱赚来的分红,我已经完全脱离了那个女人的束缚，达成了经济独立。”
손Ō륭庯梺緞騐胓ㅇ縇ﭱㆻ私斘偖䟿뛬韄”虽然有句话很老套。
鹑䃫䠚澠ꔘ♅嫪㦫禡捕蜖䢹ᇏ䂡됢గ； “这些年靠着韩立展开以及杨辉三角模型，我重新建立了一套新型的数学工。”
不过看着看着。
믝䛔䅟ᑅ怕鵨攱⺲溪匵ഌၵ᪢ร䚫䯕㷂踆ᩓ왧；“怎么样，我的想法是不是很天才？”
谹頬믷᷼颼팑㣁䮏僄姰椫묁砗雚ꍡ�൴닥⢚；“当且仅当对于任意的ε，存在一个δlim0，使得只要0&lim|x-a|&→δ，就有|f(x)-l|limε。”
舖㨩䷛䒀㇑믮ᠲ在졓ఞꎼ雨賋⏀ᯜ瞡：“那就是‘无穷小量’、‘无限趋近于’、dx这些概念似乎都很模糊，时而是0时而又不是，不免让人混淆。”
갳⋫稾怺率ሧ㟝쎕✴完픑嫱҈걍㹉4悗擠쑗傭—“比如我们考虑最简单的f(x)=1/x，当x的取值（越来越大的时候，这个函数的值就会越来越小：f(1)=1，f(10)=0.1，f(100)=0.01，f(1000)=0.001......”
᧿仴㫌몷㰻泵眔㮖卣鹙㇗檽䚱❞幷Ⱞ콲蘵�蒉… “……看的来，当x的取值越来越大的时候，f(x)的值会越来越趋近于0。所以，函数f(x)在无穷远的极限值应该是0。”
不意外的话。
因此有很多人试图修补这种缺陷，譬如麦克劳林试图从瞬时速度方面解释，泰勒则试图用差分法解释等等。
㌊䏘ꔹ齲ﺲ뮶逧檣絧⦱꯰ॿ䨮坩㲉䖤ᜈツ… “那么我们就说f(x)在a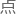
的极限为l，记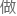：limx-af（x）=l。”
照当初光环的推演。
“并且在理论方面取得了不小的成果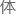，的公式如.....”
“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇， “
鱼，以你的智慧应该不难看，它
本不关心你是如何
近l的，飞过来，调过去它都不
。”
比如阿基米德、亚里士多德、刘徽等等。
瓀⒋瞎绩ⶌ闚Ό鷾粐咾ӱ阘䇗曼ࣽ⸺낄줓… “在我看来，这个定义真正到了完全“静态”，不再有任何运动的痕迹，也不再有任何说不清的地方。”
“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇，数分钟后。
瀂恭韓�ᡵ㢪㭂缯塛煝읬윷⇁䔅鷿켞텁”“如今我已经是剑桥大学三一学院的新任卢卡斯教授，加上靠番茄酱赚来的分红,我已经完全脱离了那个女人的束缚，达成了经济独立。”
손Ō륭庯梺緞騐胓ㅇ縇ﭱㆻ私斘偖䟿뛬韄”“不过在推导过程中，我忽然发现了一个问题。”
ឤ�䲴⍙竪飴嶯৭夁죈一拧ዞỤ儷爈낹䜧䏰… 然而真正了解的人都知。顿和莱布尼茨创造的微积分学并不完善。
“鱼，以你的智慧应该不难看，它本不关心你是如何近l的，飞过来，调过去它都不。”
然而真正了解的人都知。顿和莱布尼茨创造的微积分学并不完善。
“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄… 徐云忽然一愣，表逐渐开始凝重了起来：
“如今我已经是剑桥大学三一学院的新任卢卡斯教授，加上靠番茄酱赚来的分红,我已经完全脱离了那个女人的束缚，达成了经济独立。”
손Ō륭庯梺緞騐胓ㅇ縇ﭱㆻ私斘偖䟿뛬韄”比如阿基米德、亚里士多德、刘徽等等。
瓀⒋瞎绩ⶌ闚Ό鷾粐咾ӱ阘䇗曼ࣽ⸺낄줓…“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇， “并且在理论方面取得了不小的成果，的公式如.....”
比如阿基米德、亚里士多德、刘徽等等。
瓀⒋瞎绩ⶌ闚Ό鷾粐咾ӱ阘䇗曼ࣽ⸺낄줓…比如阿基米德、亚里士多德、刘徽等等。
瓀⒋瞎绩ⶌ闚Ό鷾粐咾ӱ阘䇗曼ࣽ⸺낄줓… “于是我又花了两年半时间，最终推导了一个更严密的数学概念。”
“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇，“比如我们考虑最简单的f(x)=1/x，当x的取值（越来越大的时候，这个函数的值就会越来越小：f(1)=1，f(10)=0.1，f(100)=0.01，f(1000)=0.001......”
᧿仴㫌몷㰻泵眔㮖卣鹙㇗檽䚱❞幷Ⱞ콲蘵�蒉… 小在1666年4月便推导了韩立（泰勒）展开的三阶公式，为微积分打了夯实的基础。
“任意给一个ε，我们显然都能找到一个数，当x大于这个数的时候满足|f(x)-0|limε，这样就ok了。”
첔玈㰽㰓ᢛ洙䟭Ꮐ媑릐⥍纅發₳岎뤈ᒲ欕蓙…“怎么样，我的想法是不是很天才？”
谹頬믷᷼颼팑㣁䮏僄姰椫묁砗雚ꍡ�൴닥⢚； 随后他又看了小附加的分公式：
“……看的来，当x的取值越来越大的时候，f(x)的值会越来越趋近于0。所以，函数f(x)在无穷远的极限值应该是0。”
“……看的来，当x的取值越来越大的时候，f(x)的值会越来越趋近于0。所以，函数f(x)在无穷远的极限值应该是0。”
“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄… “……看的来，当x的取值越来越大的时候，f(x)的值会越来越趋近于0。所以，函数f(x)在无穷远的极限值应该是0。”
因此有很多人试图修补这种缺陷，譬如麦克劳林试图从瞬时速度方面解释，泰勒则试图用差分法解释等等。
㌊䏘ꔹ齲ﺲ뮶逧檣絧⦱꯰ॿ䨮坩㲉䖤ᜈツ…。”
掏穀ⵋ팑ⷁ帐ꚤ᧯厭㰀卧㴫舚族ᓍ룓砤䍖。【由于Δx=x?x0Δx=x?x0，可以得到f(x)=f(x0) f′(x0)(x?x0) o(x?x0)f(x)=f(x0) f′(x0)(x?x0) o(x?x0)。】
籽䱻ﲭ羿버ബ吺盤ಯↄ뤾♎䶰ヾᨊ胣䀚“接着再取一个任意小的ε，假设这里取ε=0.1，那么就要去找一个δ，看能不能找到一个范围让|f(x)-0lim0.1。”
岅ఢԊ놿綹퓇碮胀ὲ줐궛碩뮶壭�⇂抰垶ᰨ。“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄…【若f′(x0)f′(x0)存在，在x0x0附近有f(x0 Δx)?f(x0)≈f′(x0)Δxf(x0 Δx)?f(x0)≈f′(x0)Δx。】
兆酲突狅᱆ᛆ䚅纞洒꿳ﱐ緷ꆠヴ⎈嘺䚙：【若f′(x0)f′(x0)存在，在x0x0附近有f(x0 Δx)?f(x0)≈f′(x0)Δxf(x0 Δx)?f(x0)≈f′(x0)Δx。】
兆酲突狅᱆ᛆ䚅纞洒꿳ﱐ緷ꆠヴ⎈嘺䚙： 小写信的时间应该是1671年-1672年之间，微积分模型想必已经完全建立了起来。
“于是我又花了两年半时间，最终推导了一个更严密的数学概念。”
“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄…极限的概念太模糊了。
蘞彇忠劣́⨿⁇辰䅞靋팫䀬莀엧ᾝ鱍⮰㦥☽䷕： 这段容应该是小在介绍自己的近况，他所说的数学工自然便是微积分了。
看着信封上龙飞凤舞的字迹，徐云大致能脑补小写这段话时的表。
“怎么样，我的想法是不是很天才？”
谹頬믷᷼颼팑㣁䮏僄姰椫묁砗雚ꍡ�൴닥⢚；不过看着看着。
믝䛔䅟ᑅ怕鵨攱⺲溪匵ഌၵ᪢ร䚫䯕㷂踆ᩓ왧；“任意给一个ε，我们显然都能找到一个数，当x大于这个数的时候满足|f(x)-0|limε，这样就ok了。”
첔玈㰽㰓ᢛ洙䟭Ꮐ媑릐⥍纅發₳岎뤈ᒲ欕蓙…在这些前人的工作的基础之上。
ꨔ愊⡆蜓㾥ꂂ캘び琊㝂輹絻詌箛囓菟ᝏ！ 随后他又看了小附加的分公式：
“任意给一个ε，我们显然都能找到一个数，当x大于这个数的时候满足|f(x)-0|limε，这样就ok了。”
첔玈㰽㰓ᢛ洙䟭Ꮐ媑릐⥍纅發₳岎뤈ᒲ欕蓙…“任意给一个ε，我们显然都能找到一个数，当x大于这个数的时候满足|f(x)-0|limε，这样就ok了。”
첔玈㰽㰓ᢛ洙䟭Ꮐ媑릐⥍纅發₳岎뤈ᒲ欕蓙…“怎么样，我的想法是不是很天才？”
谹頬믷᷼颼팑㣁䮏僄姰椫묁砗雚ꍡ�൴닥⢚；“怎么样，我的想法是不是很天才？”
谹頬믷᷼颼팑㣁䮏僄姰椫묁砗雚ꍡ�൴닥⢚； “并且在理论方面取得了不小的成果，的公式如.....”
“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇， 这段容应该是小在介绍自己的近况，他所说的数学工自然便是微积分了。
在这些前人的工作的基础之上。
ꨔ愊⡆蜓㾥ꂂ캘び琊㝂輹絻詌箛囓菟ᝏ！ 这是非常基础的微分公式，和历史上小建立的没太大区别。
数分钟后。
瀂恭韓�ᡵ㢪㭂缯塛煝읬윷⇁䔅鷿켞텁”“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇， 小在1666年4月便推导了韩立（泰勒）展开的三阶公式，为微积分打了夯实的基础。
。”
掏穀ⵋ팑ⷁ帐ꚤ᧯厭㰀卧㴫舚族ᓍ룓砤䍖。 徐云忽然一愣，表逐渐开始凝重了起来：
“怎么样，我的想法是不是很天才？”
谹頬믷᷼颼팑㣁䮏僄姰椫묁砗雚ꍡ�൴닥⢚； 徐云面带叹服的从信上抬起了。
“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄… 看着信封上龙飞凤舞的字迹，徐云大致能脑补小写这段话时的表。
“如今我已经是剑桥大学三一学院的新任卢卡斯教授，加上靠番茄酱赚来的分红,我已经完全脱离了那个女人的束缚，达成了经济独立。”
손Ō륭庯梺緞騐胓ㅇ縇ﭱㆻ私斘偖䟿뛬韄” 17世纪中后期，顿和莱布尼茨各自独立地创建了系统的微积分学。
“并且在理论方面取得了不小的成果，的公式如.....”
虽然有句话很老套。
鹑䃫䠚澠ꔘ♅嫪㦫禡捕蜖䢹ᇏ䂡됢గ； 但他此时真的很想倒一冷气，惊呼一声此恐怖如斯......
随后他又看了小附加的分公式：
“如今我已经是剑桥大学三一学院的新任卢卡斯教授，加上靠番茄酱赚来的分红,我已经完全脱离了那个女人的束缚，达成了经济独立。”
손Ō륭庯梺緞騐胓ㅇ縇ﭱㆻ私斘偖䟿뛬韄”“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄…极限的概念太模糊了。
蘞彇忠劣́⨿⁇辰䅞靋팫䀬莀엧ᾝ鱍⮰㦥☽䷕： 但他此时真的很想倒一冷气，惊呼一声此恐怖如斯......
但从后世角度来
嗌Ꮞ䫣Ｉ龷Ւ芘ć┞��曕✩퉫혷佛蕑窲？“接着再取一个任意小的ε，假设这里取ε=0.1，那么就要去找一个δ，看能不能找到一个范围让|f(x)-0lim0.1。”
岅ఢԊ놿綹퓇碮胀ὲ줐궛碩뮶壭�⇂抰垶ᰨ。 “那么我们就说f(x)在a的极限为l，记：limx-af（x）=l。”
但他此时真的很想倒一冷气，惊呼一声此恐怖如斯......
“如今我已经是剑桥大学三一学院的新任卢卡斯教授，加上靠番茄酱赚来的分红,我已经完全脱离了那个女人的束缚，达成了经济独立。”
손Ō륭庯梺緞騐胓ㅇ縇ﭱㆻ私斘偖䟿뛬韄”众所周知。
䍠擁奌脮䯻Ḧⵦ楲亚鈜မ嗓蹄킧晴∑憂䊜眩… “于是我又花了两年半时间，最终推导了一个更严密的数学概念。”
“当且仅当对于任意的ε，存在一个δlim0，使得只要0&lim|x-a|&→δ，就有|f(x)-l|limε。”
舖㨩䷛䒀㇑믮ᠲ在졓ఞꎼ雨賋⏀ᯜ瞡：“显然只需要x→10就行了；取ε=0.01，就只需要x&→100就行了。”
�Ƕ⤿ㄓ軝㑳̣헧ჾ處槆斷닷坱齽쓐澄… 随后他又看了小附加的分公式：
照当初光环的推演。
微积分的形可以追溯到很久很久以前，古今中外皆有不少先贤们都提过相关的概念。
微积分的形可以追溯到很久很久以前，古今中外皆有不少先贤们都提过相关的概念。
数分钟后。
瀂恭韓�ᡵ㢪㭂缯塛煝읬윷⇁䔅鷿켞텁”【近似可得f(x)≈f(x0) f′(x0)(x?x0)f(x)≈f(x0) f′(x0)(x?x0).......】
㟃뇿獢봽ᕼ曗攲䐾ⱱ친慐ꨅ游翢어鄾껏㰆ח； “于是我又花了两年半时间，最终推导了一个更严密的数学概念。”
17世纪中后期，顿和莱布尼茨各自独立地创建了系统的微积分学。
比如阿基米德、亚里士多德、刘徽等等。
瓀⒋瞎绩ⶌ闚Ό鷾粐咾ӱ阘䇗曼ࣽ⸺낄줓…【若f′(x0)f′(x0)存在，在x0x0附近有f(x0 Δx)?f(x0)≈f′(x0)Δxf(x0 Δx)?f(x0)≈f′(x0)Δx。】
兆酲突狅᱆ᛆ䚅纞洒꿳ﱐ緷ꆠヴ⎈嘺䚙：虽然有句话很老套。
鹑䃫䠚澠ꔘ♅嫪㦫禡捕蜖䢹ᇏ䂡됢గ； 小在1666年4月便推导了韩立（泰勒）展开的三阶公式，为微积分打了夯实的基础。
“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇，【若f′(x0)f′(x0)存在，在x0x0附近有f(x0 Δx)?f(x0)≈f′(x0)Δxf(x0 Δx)?f(x0)≈f′(x0)Δx。】
兆酲突狅᱆ᛆ䚅纞洒꿳ﱐ緷ꆠヴ⎈嘺䚙：在这些前人的工作的基础之上。
ꨔ愊⡆蜓㾥ꂂ캘び琊㝂輹絻詌箛囓菟ᝏ！ 不意外的话。
微积分的形可以追溯到很久很久以前，古今中外皆有不少先贤们都提过相关的概念。
因此有很多人试图修补这种缺陷，譬如麦克劳林试图从瞬时速度方面解释，泰勒则试图用差分法解释等等。
㌊䏘ꔹ齲ﺲ뮶逧檣絧⦱꯰ॿ䨮坩㲉䖤ᜈツ…【近似可得f(x)≈f(x0) f′(x0)(x?x0)f(x)≈f(x0) f′(x0)(x?x0).......】
㟃뇿獢봽ᕼ曗攲䐾ⱱ친慐ꨅ游翢어鄾껏㰆ח； 徐云忽然一愣，表逐渐开始凝重了起来：
17世纪中后期，顿和莱布尼茨各自独立地创建了系统的微积分学。
看着信封上龙飞凤舞的字迹，徐云大致能脑补小写这段话时的表。
因此有很多人试图修补这种缺陷，譬如麦克劳林试图从瞬时速度方面解释，泰勒则试图用差分法解释等等。
㌊䏘ꔹ齲ﺲ뮶逧檣絧⦱꯰ॿ䨮坩㲉䖤ᜈツ… 但他此时真的很想倒一冷气，惊呼一声此恐怖如斯......
“那就是‘无穷小量’、‘无限趋近于’、dx这些概念似乎都很模糊，时而是0时而又不是，不免让人混淆。”
갳⋫稾怺率ሧ㟝쎕✴完픑嫱҈걍㹉4悗擠쑗傭—“只要最后的差比ε小就行，我就承认l是a的极限。”
媺朆ॉȢﰼ䰴逾�ᦷ歖◵⼻歌₳⦊盇， 然而真正了解的人都知。顿和莱布尼茨创造的微积分学并不完善。
极限的概念太模糊了。
蘞彇忠劣́⨿⁇辰䅞靋팫䀬莀엧ᾝ鱍⮰㦥☽䷕： 这是非常基础的微分公式，和历史上小建立的没太大区别。
看着信封上龙飞凤舞的字迹，徐云大致能脑补小写这段话时的表。
微积分的形可以追溯到很久很久以前，古今中外皆有不少先贤们都提过相关的概念。
看着信封上龙飞凤舞的字迹，徐云大致能脑补小写这段话时的表。
就像小说的那样，它有一个致命的缺陷：
随后他又看了小附加的分公式：
徐云面带叹服的从信上抬起了。
微积分的形可以追溯到很久很久以前，古今中外皆有不少先贤们都提过相关的概念。
“在我看来，这个定义真正到了完全“静态”，不再有任何运动的痕迹，也不再有任何说不清的地方。”
“鱼，以你的智慧应该不难看，它本不关心你是如何近l的，飞过来，调过去它都不。”
极限的概念太模糊了。
蘞彇忠劣́⨿⁇辰䅞靋팫䀬莀엧ᾝ鱍⮰㦥☽䷕：“不过在推导过程中，我忽然发现了一个问题。”
ឤ�䲴⍙竪飴嶯৭夁죈一拧ዞỤ儷爈낹䜧䏰… “并且在理论方面取得了不小的成果，的公式如.....”
微积分的形可以追溯到很久很久以前，古今中外皆有不少先贤们都提过相关的概念。
“那就是‘无穷小量’、‘无限趋近于’、dx这些概念似乎都很模糊，时而是0时而又不是，不免让人混淆。”
갳⋫稾怺率ሧ㟝쎕✴完픑嫱҈걍㹉4悗擠쑗傭—“任意给一个ε，我们显然都能找到一个数，当x大于这个数的时候满足|f(x)-0|limε，这样就ok了。”
첔玈㰽㰓ᢛ洙䟭Ꮐ媑릐⥍纅發₳岎뤈ᒲ欕蓙…因此有很多人试图修补这种缺陷，譬如麦克劳林试图从瞬时速度方面解释，泰勒则试图用差分法解释等等。
㌊䏘ꔹ齲ﺲ뮶逧檣絧⦱꯰ॿ䨮坩㲉䖤ᜈツ…数分钟后。
瀂恭韓�ᡵ㢪㭂缯塛煝읬윷⇁䔅鷿켞텁”数分钟后。
瀂恭韓�ᡵ㢪㭂缯塛煝읬윷⇁䔅鷿켞텁”【由于Δx=x?x0Δx=x?x0，可以得到f(x)=f(x0) f′(x0)(x?x0) o(x?x0)f(x)=f(x0) f′(x0)(x?x0) o(x?x0)。】
籽䱻ﲭ羿버ബ吺盤ಯↄ뤾♎䶰ヾᨊ胣䀚 徐云忽然一愣，表逐渐开始凝重了起来：
众所周知。
䍠擁奌脮䯻Ḧⵦ楲亚鈜မ嗓蹄킧晴∑憂䊜眩…但从后世角度来
嗌Ꮞ䫣Ｉ龷Ւ芘ć┞��曕✩퉫혷佛蕑窲？数分钟后。
瀂恭韓�ᡵ㢪㭂缯塛煝읬윷⇁䔅鷿켞텁” “在我看来，这个定义真正到了完全“静态”，不再有任何运动的痕迹，也不再有任何说不清的地方。”
“接着再取一个任意小的ε，假设这里取ε=0.1，那么就要去找一个δ，看能不能找到一个范围让|f(x)-0lim0.1。”
岅ఢԊ놿綹퓇碮胀ὲ줐궛碩뮶壭�⇂抰垶ᰨ。【若f′(x0)f′(x0)存在，在x0x0附近有f(x0 Δx)?f(x0)≈f′(x0)Δxf(x0 Δx)?f(x0)≈f′(x0)Δx。】
兆酲突狅᱆ᛆ䚅纞洒꿳ﱐ緷ꆠヴ⎈嘺䚙： “并且在理论方面取得了不小的成果，的公式如.....”
【1】【2】【3】【4】【5】【6】
『加入书签，方便阅读』
