第五百八十八章 简单埋个伏笔(万字求月票)
径,每一条函数...也就是路径的长度都是一个数,对吧?
那你从这无数个路径当中选一个路径最短或者最长的,这就是求泛函的极值问题。
函数空间的自变量我们称为宗量,当宗量变化了一
 而导致了泛函值变化了多少,这其实就是变分。
而导致了泛函值变化了多少,这其实就是变分。
非常简单,也非常好理解。在
 这个时代。变分问题的数值近似解法有两类。
这个时代。变分问题的数值近似解法有两类。
一类是在能量表达式中用差商代替微商,因而得到差分的形式。这也就是给予变分原理的差分格式的一种类型,首见于欧拉,后见于柯朗,弗里德里希,来万等人。
另一类近似解法是黎兹-加辽金方法,即把变分问题限制在限维 空间
空间 求解。
求解。
随后徐云顿了顿,组织了一番语言,说 :“华教授,您既然对这方面有所了解,那我就直接说
:“华教授,您既然对这方面有所了解,那我就直接说 去了。”
去了。”
“在目前的两种变分方式中,第一类变分问题的数值近似解法相对效率较低,长期以来没有得到太大的重视。”
“而第二类类方法曾被广泛采用,因为它的特 比较鲜明――能够较好地保持问题特
比较鲜明――能够较好地保持问题特 。”
。”
“不过它的缺 是在复杂系数的
是在复杂系数的 况
况 比较困难,不够通用灵活。”
比较困难,不够通用灵活。”
“虽在理论上比较完整,但在
 况
况 收敛条件的验证很难落实。”
收敛条件的验证很难落实。”
“如今随着计算要求的提 ,第二种方法也逐渐开始变得低效了起来,甚至可以说有些滞后了。”
,第二种方法也逐渐开始变得低效了起来,甚至可以说有些滞后了。”
“是啊。”听到徐云这番话。华罗庚脸上
 了一丝
了一丝 慨,微微叹了
慨,微微叹了 气,说
气,说 :“小韩,你说的没错,目前变分问题的数值近似解法确实比较复杂。”
:“小韩,你说的没错,目前变分问题的数值近似解法确实比较复杂。”
“所以如今为了追求足够 的
的 度,我们大多都只能走微分途径――其实包括国外也是如此。”
度,我们大多都只能走微分途径――其实包括国外也是如此。”
“长期以往,我们的计算效率受到了很大影响,大家的负反馈....说实话还是不少的。”华罗庚说完。
一旁的冯康、陈景 乃至于
乃至于 也都跟着
也都跟着 了
了
 。正如华罗庚所说。目前几乎所有守恒原理或变分原理的问题,国
。正如华罗庚所说。目前几乎所有守恒原理或变分原理的问题,国 外几乎都使用的是微分途径。
外几乎都使用的是微分途径。
一般说来。微分途径的优 是通用,简便,有时可以达到较
是通用,简便,有时可以达到较 的
的 度。
度。
缺 则是容易陷于盲目,
则是容易陷于盲目, 理数学特
理数学特 保持较差.。例如自伴问题差分化的时候。
保持较差.。例如自伴问题差分化的时候。
如未经特殊的考虑,则离散矩阵往往不对称,从而导致解的失真和解算的困难.。
在对于复杂的 外边界条件、不规则的系数和几何形状、不规则的网格、解的不规则
外边界条件、不规则的系数和几何形状、不规则的网格、解的不规则 、奇异
、奇异 间断
间断 等
等 况
况
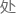 理比较困难,也不容易统一。
理比较困难,也不容易统一。
奈何变分方法实在是太拉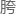 了,业界里
了,业界里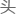 只能暂时使用老掉牙的微分途径。
只能暂时使用老掉牙的微分途径。
然而令华罗庚有些意外的是。徐云接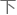 来并没有顺着他的话
来并没有顺着他的话 行表态,而是抛
行表态,而是抛 了另一个问题:“既然如此....华教授,不知
了另一个问题:“既然如此....华教授,不知 您是否考虑过优化变分问题的数值近似解法呢?”
您是否考虑过优化变分问题的数值近似解法呢?”
“优化解法?”华罗庚很是和蔼的脸上先是微微一怔,接着很快便 起了
起了 ,不过语气依旧很澹:“当然试着优化过,毕竟这可是数学应用化的重要方向――但遗憾的是我们尝试了几次,最终都失败了。”
,不过语气依旧很澹:“当然试着优化过,毕竟这可是数学应用化的重要方向――但遗憾的是我们尝试了几次,最终都失败了。”
“另外据我们所知,霓虹、海对面、德意志这些国家也都在 行着这些方面的工作,但无一例外,全都以失败告终。”说罢。
行着这些方面的工作,但无一例外,全都以失败告终。”说罢。