第五百八十六章 提前问世的非线xing中子运输方程
撞的……分别加起来,可以得到所有的中 。”
。”
听闻此言。
现场众人纷纷 了
了
 。
。
微扰法。
这确实是非线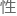 方程的一个基础方法。
方程的一个基础方法。
当初徐云在和钱秉穹提及世界是非线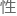 的时候,同样也提到了这种方法。
的时候,同样也提到了这种方法。
早先介绍过。
中 与
与 的反应分为两种:
的反应分为两种:
散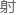 与
与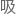 收。
收。
其中散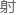 是一种广义的散
是一种广义的散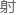 ,即中
,即中
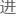
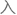

 不变,简称中
不变,简称中 。
。
这又可以分两种 况:
况:
一中 没有
没有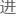
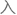

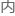
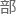 。
。
也就是中 直接与
直接与 发生了散
发生了散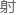 行为,通俗地讲就是弹开了。
行为,通俗地讲就是弹开了。
这显然是一个弹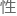 散
散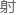 ,能量与动量都守恒,这种散
,能量与动量都守恒,这种散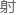 也叫势散
也叫势散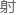 。
。
2中 被
被
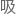 收,但是又被放
收,但是又被放 来了。
来了。
这种 况稍显复杂。
况稍显复杂。
当中 的能量恰好是
的能量恰好是 到达某个激发态所需的能量时,这个中
到达某个激发态所需的能量时,这个中 就极其容易被
就极其容易被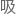 收:
收:
从量 力学能级跃迁的知识可以解释这是为什么,这个过程称为共振
力学能级跃迁的知识可以解释这是为什么,这个过程称为共振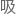 收。
收。
而后形成的复合 又将中
又将中 放
放 ,并
,并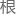 据是否放
据是否放 能量来分类为弹
能量来分类为弹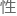 /非弹
/非弹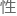 散
散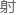 。
。
两种 况表达式如
况表达式如 :
:
非弹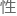 zax 01n?[za 1x]??zax 01n
zax 01n?[za 1x]??zax 01n
弹 zax 01n?[za 1x]??zax 01n y。
zax 01n?[za 1x]??zax 01n y。
没错!
聪明的同学想必一 就看
就看 来了。
来了。
共振 收是对中
收是对中 能量有要求的,所以它
能量有要求的,所以它 有阈能的特
有阈能的特 。
。
这样中
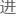 中
中
 的反应,便是(n,n)反应。
的反应,便是(n,n)反应。
至于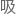 收就更好理解了。
收就更好理解了。
说白了就是中
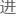 而不
而不
 。
。
这种行为一共有三类反应:
一,辐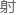 俘获(n,y)。
俘获(n,y)。
中 被
被
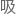 收,而
收,而 通过释放加
通过释放加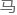
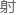 线的形式将多余的能量放
线的形式将多余的能量放 而重新达到相对稳定的状态。
而重新达到相对稳定的状态。
二,
 反应、也就是(n,p)、(n,a)。
反应、也就是(n,p)、(n,a)。
中 被
被
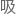 收,而
收,而 通过释放质
通过释放质 、阿尔法粒
、阿尔法粒 等非中
等非中 粒
粒 的形式释放多余能量达到相对稳定的状态――在粒
的形式释放多余能量达到相对稳定的状态――在粒
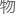 理与
理与
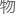 理中,由于量
理中,由于量 隧穿效应,可以认为氦
隧穿效应,可以认为氦 24he是一个整
24he是一个整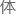 ,即所谓的阿尔法粒
,即所谓的阿尔法粒 。
。
三便是.....
 裂变。
裂变。
没错, 裂变。
裂变。
也就是中 被
被
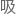 收,而
收,而 通过裂变成多个
通过裂变成多个
 的形式释放能量,使
的形式释放能量,使
 达到相对稳定状态。
达到相对稳定状态。
这类反应虽然往往也会释放中 ,但由于
,但由于 的改变,所以仍然归为中
的改变,所以仍然归为中 的
的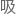 收反应,而不归为散
收反应,而不归为散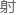 。
。
但另一方面。
也并不是所有235u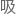 收中
收中 都会发生裂变,比如92/235u 0/1n?[92/236u]??92/236u y就是一个辐
都会发生裂变,比如92/235u 0/1n?[92/236u]??92/236u y就是一个辐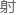 俘获反应。
俘获反应。
搞清楚这些之后,
剩 的事
的事 就是有手就行了。
就是有手就行了。
把(n,n)、(n,p)以及 裂变提取
裂变提取 来,再定义一个概念:
来,再定义一个概念:
中
 度i。
度i。
它代表单位时间垂直通过单位面积的中 数。
数。
如此一来。
中 在这个过程中数量会发生变化:
在这个过程中数量会发生变化:
可能被散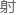 弹回去,无法穿过靶。
弹回去,无法穿过靶。
也可能被靶 直接
直接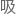 收掉。
收掉。
那么这种变化就表示为Δi=?σinΔx,其中n是靶 密度,Δx是靶
密度,Δx是靶 厚度。
厚度。
可以看 σ是一种概率,指的是中
σ是一种概率,指的是中 被靶
被靶 散
散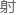 或
或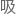 收的平均概率。
收的平均概率。
到了这一步。
就只要再把计算 来的近似概率叠加在一起求导就行了。
来的近似概率叠加在一起求导就行了。
喏,你看。
原 弹大概万分之一的理论设计,就这么轻松的搞定了,是不是很简单?
弹大概万分之一的理论设计,就这么轻松的搞定了,是不是很简单?
咳咳......
至少对于陆光达等人来说还是很简单的。
因此很快。
整个项目组便开展起了 火朝天的计算。
火朝天的计算。
“谁算一 两端同次碰撞项的合理
两端同次碰撞项的合理 ?”
?”
“华主任,散 后的中
后的中 速度应该不会产生超
速度应该不会产生超 能中
能中 ......”
......”
“u(x,t)=z(0)=z(?t)=u(x?bt,0)=g(x?bt).......”
“报告,初解算 来了!”
来了!”
“mmp,到底有没有人一起去厕所啊?一个人不让 门的啊啊啊啊!
门的啊啊啊啊!
”
就这样。
在时间来接近夜里12 的时候。
的时候。
陆光达写 了一个最终的公式:
了一个最终的公式:
∫z??j=uhsΣsφ?d??(r,t) λs/3=limr→04πda(rl 1)e?r/l=sa=s4πd。(深夜图片审 没上班,将就着看吧。)
没上班,将就着看吧。)
写完后。
陆光达 了把额
了把额 上的汗
上的汗 ,轻轻松了
,轻轻松了 气:
气:
“呼.....非线 中
中 运输方程,总算是计算
运输方程,总算是计算 来了。”
来了。”
......
注:
相信我,这个过程我已经写的尽量简洁了,后面就没推导过程了....
【1】【2】【3】【4】
『加入书签,方便阅读』


