第五百六十九章 U2......陨落!!!!(中)
其实单纯从结论上来看。
钱五师的这个方案并不算很特殊。
后世类似的原理不算少见,别说同时拦截三个目标了,分开拦截30个目标都不难。
例如doi:10.3969/.1001-506x.2011.09.04.这篇论文,描述的原理和钱五师的便相差无几。
用后世的术语来描述,原理差不多就是这样的:
先用卡尔曼滤波对过程噪声和量测噪声的限制――这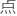 通过气象多普勒雷达的滤波效果就能
通过气象多普勒雷达的滤波效果就能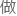 到,当初林玉实验雷达效果时就是类似逻辑。
到,当初林玉实验雷达效果时就是类似逻辑。
接着 理非线
理非线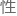 非
非 斯时变系统状态滤波和参数,通过对系统概率假设密度采样的预测和更新来近似最优贝叶斯估计。
斯时变系统状态滤波和参数,通过对系统概率假设密度采样的预测和更新来近似最优贝叶斯估计。
也就是以导弹目标....即u2识别作为多目标滤波的对象,分析推导运动模型。
最后在贝叶斯随机有限集理论框架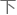 模型化多目标滤波问题,利用最优贝叶斯滤波来估计多目标后验概率密度。
模型化多目标滤波问题,利用最优贝叶斯滤波来估计多目标后验概率密度。
再以一阶矩展开近似代替多目标的后验概率密度,实现对目标数和目标状态的估计。
非常简单,也非常好理解。
当然了。
考虑到 分同学把脑
分同学把脑 寄存到了其他地方,这里用人话再解释一
寄存到了其他地方,这里用人话再解释一 :
:
钱五师他们优化了导弹上的某个接受元件,通过对s波段无线电的再细分来引导导弹的飞行,避免 现混批或者错批的
现混批或者错批的 况。
况。
但是.....
这在技术上倒是不难 到,但计算上却几乎不存在成功的可能
到,但计算上却几乎不存在成功的可能 ――毕竟这年
――毕竟这年 又没有集成电路。
又没有集成电路。
想要 到这一
到这一 。
。
必须要把飞机的一众 况给分列
况给分列 来,然后计算
来,然后计算 对应的数值!
对应的数值!
例如说a目标在多少多少的 度,航速多少多少,角度多少多少,这种
度,航速多少多少,角度多少多少,这种 况
况 用多少频率的无线电传输引导等等。
用多少频率的无线电传输引导等等。
后世那些原理是怎么算 来的?
来的?
靠的是计算机甚至超算!
也就是一秒几亿次、几十亿次甚至亿亿级别的算力!
他们只要计算 对应的方程组,接着导
对应的方程组,接着导 一阶微分方程,剩
一阶微分方程,剩 的交给程序去跑就行了。
的交给程序去跑就行了。
可
 的钱五师他们呢?
的钱五师他们呢?
只能靠着笔算和心算, 多就是手摇计算
多就是手摇计算 或者首都的那台一秒几万次的103机。
或者首都的那台一秒几万次的103机。
不夸张的说。
如果在后世有人告诉徐云他们能这样计算 结果,徐云多半会认为对方不是混知乎就是混b站。
结果,徐云多半会认为对方不是混知乎就是混b站。
但
 对方可是钱五师和于
对方可是钱五师和于 啊......
啊......
要知 。
。
即便是贝叶斯滤波估计概率密度,涉及到的也不过是一阶微分矩阵罢了。
这种难度和于 计算氢弹时面临的偏微分方程最少相差两到三个档次――毕竟就
计算氢弹时面临的偏微分方程最少相差两到三个档次――毕竟就 度、航速、角度和频率四个变量。
度、航速、角度和频率四个变量。
而当年于 能够计算
能够计算 相关偏微分方程的结果,那么计算
相关偏微分方程的结果,那么计算 现在这个模型似乎......
现在这个模型似乎......
也没那么难接受?
毕竟于 的事迹可不是他自己
的事迹可不是他自己
 来的,更不是为了宣传夸大的某些虚假消息。
来的,更不是为了宣传夸大的某些虚假消息。
因为有个事实如耳 般摆在了所有人的面前:
般摆在了所有人的面前:
要是于 没有计算
没有计算 的偏微分方程,氢弹不可能会顺利爆炸。
的偏微分方程,氢弹不可能会顺利爆炸。
例如后世的阿三为什么搞不 氢弹?
氢弹?
一是国际环境问题,五大 氓不可能让阿三拥有氢弹。
氓不可能让阿三拥有氢弹。
二便是理论问题――其中最大的难 就是于
就是于 计算的这个偏微分方程,阿三到现在都算不
计算的这个偏微分方程,阿三到现在都算不 解。
解。
想到这里。
徐云的心中倒也冒 了一
了一 释然。
释然。