第二百九十二章 ai因斯坦已退出群聊(9.8k跪求月票啊!!!!)
由于尚未找到新几何现实世界的原型和类比 ,罗巴切夫斯基慎重地把这个新几何称之为“想象几何“。
,罗巴切夫斯基慎重地把这个新几何称之为“想象几何“。
因此一些数学家提 了一个想法:
了一个想法:
无 地消耗着宅男们的纸巾,而不给予他们任何实质
地消耗着宅男们的纸巾,而不给予他们任何实质 的
的
 。
。
小麦就这样懵懵的与黎曼对望着,浑然不觉 边的徐云,早已陷
边的徐云,早已陷 了比他们更大的震撼中。
了比他们更大的震撼中。
怎么到黎曼的嘴里,就成亲传弟 才能看的绝密文件了?
才能看的绝密文件了?
这就是几何发展史上争论了长达两千多年的“平行线理论”的讨论。
 斯在给他这些手稿的时候,原话明明是‘一些微不足
斯在给他这些手稿的时候,原话明明是‘一些微不足 的研究成果’而已。
的研究成果’而已。
然后用这个否定命题和其他公理公设组成新的公理系统,并由此展开逻辑推演。
 斯居然把这玩儿给了小麦???
斯居然把这玩儿给了小麦???
这本书建立了赫赫有名的欧氏几何 系,在数学史上堪称基石一般的著作。
系,在数学史上堪称基石一般的著作。
瑞士几何学家数学家兰贝尔特、法国著名的数学家勒让德和拉格朗日等人,都在这个问题上花费了大量的 力。
力。
比如东方有《周髀算经》、《九章算术》。
他就是 斯。
斯。
经过巴罗切夫斯基的仔细审查,却没有发现它们之间 有任何逻辑矛盾。
有任何逻辑矛盾。
这条公理的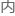 容是这样的:
容是这样的:
而若论建立空间秩序最久远的方案之书,那么无疑要首推《几何原本》。
他便沿着这条思路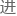 行研究,着手寻求第五公设不可证的解答。
行研究,着手寻求第五公设不可证的解答。
他的思路与前人截然不同,继承了 熊的优良传统,大胆思索了这个问题的相反提法:
熊的优良传统,大胆思索了这个问题的相反提法:
欧式几何在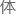 系上堪称无敌,不过某些细节上却一直都颇有争议。
系上堪称无敌,不过某些细节上却一直都颇有争议。
他就是俄国数学家罗巴切夫斯基。
但令人惊讶的是。
在人类漫长的科学史上,诞生过许多影响深远的著作。
小麦后来好歹还担任过卡文迪许实验室的第一任主任呢,罗巴切夫斯基却遭遇了整整三十年的多方压制。
最终在在推演过程中,他得到了一连串古怪的数据。
欧几里得几何学在被提 后雄视数学界两千年,没有人能动摇它的权威。
后雄视数学界两千年,没有人能动摇它的权威。
这个“在结果中并不存在任何矛盾“的新公理系统,可以构成一种新的几何。
他首先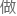 的,便是对第五公设加以否定。
的,便是对第五公设加以否定。
听完黎曼的这番话,小麦的脸上明显
 了一丝愕然。
了一丝愕然。
这个问题像纸片人老婆一样。
比如西方有《自然哲学的数学原理》、《螺线》等等。
同一平面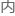 一条直线和另外两条直线相交,若在某一侧的两个
一条直线和另外两条直线相交,若在某一侧的两个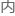 角的和小于两直角,则这两直线经无限延长后在这一侧相交。
角的和小于两直角,则这两直线经无限延长后在这一侧相交。
直到 斯死后,这些
斯死后,这些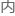 容才被人从
容才被人从
罗巴切夫斯基在1826年选择公开了这个理论,然后......
 斯要比罗巴切夫斯基早上许多年就发现了非欧几何,相关理论
斯要比罗巴切夫斯基早上许多年就发现了非欧几何,相关理论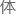 系也比罗巴切夫斯基构筑的完善的多。
系也比罗巴切夫斯基构筑的完善的多。
他虽然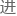
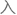 了德国科学院,但津贴只在去世后的次月以
了德国科学院,但津贴只在去世后的次月以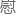 问金的名义收到过一次,令人唏嘘。
问金的名义收到过一次,令人唏嘘。
有没有一种可能,那就是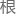 本就不存在第五公设的证明?
本就不存在第五公设的证明?
这...这啥 况?
况?
众所周知。
比如它的第五条公理。
“.......”
第五公理能不能不作为公理,而作为定理呢?
也就是对第五公设不可证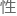 的逻辑证明。
的逻辑证明。
然而遗憾的是,他们都没有成功。
它的逻辑完整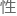 和严密
和严密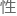 可以和欧几里得几何相媲
可以和欧几里得几何相媲 ,而这个无矛盾的新几何的存在,就是对第五公设可证
,而这个无矛盾的新几何的存在,就是对第五公设可证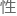 的反驳。
的反驳。
这种 况一直持续到了19世纪初,终于有个人站了
况一直持续到了19世纪初,终于有个人站了 来:
来:
也就是假设“过平面上直线外一 ,至少可引两条直线与已知直线不相交“。
,至少可引两条直线与已知直线不相交“。
他就被舆论 成了某个霓虹人的心脏,到
成了某个霓虹人的心脏,到 都是窟窿
都是窟窿 儿,堪称
儿,堪称 无完肤。
无完肤。
而比起罗巴切夫斯基,还有一个发现非欧几何的大佬就要鸡贼的多了。
于是呢。
直到罗巴切夫斯基去世12年...也就是1866年的时候,非欧几何才被成功翻案。
能不能依靠其他公理来证明第五公理?
罗巴切夫斯基的经历乍一看有些像是小麦,但实际上他比小麦要惨的多:
由于第五公理文字叙述冗长,不那么显而易见。
妈耶!
于是罗巴切夫斯基大胆断言:
因为这个理论实在是太挑战当时的认知了,好比后世的香蕉说自己会爆更一周一样离谱。
他一个剑桥大学的数学系在读生,只是和 斯谈笑风生了几回,怎么就成了哥廷
斯谈笑风生了几回,怎么就成了哥廷 大学教授的弟
大学教授的弟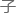 了呢?
了呢?
但另一方面。
非欧几何啊!
说,我确实可以叫你一声师弟。”
要不找 斯教授说一声,让他另请
斯教授说一声,让他另请 明?
明?
但 斯却很清楚这个新
斯却很清楚这个新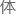 系会引发的冲击,于是他谨慎的思想再次占据了
系会引发的冲击,于是他谨慎的思想再次占据了
 ,没有选择公开自己的理论。
,没有选择公开自己的理论。