经到了最终验的阶段了。

        到底能不能找到那颗“柯南星”，尽皆在此一举！

        随后黎曼将收缴好的文件搬到了斯面前，恭敬说：

        “老师，一共218份记录，都在归纳好了。”

        斯朝他了，示意他放到自己面前。

        在此前的轨辨识过程中，斯一直在边上坐着养神，没有参与计算过程。

        这并不是因为他已经年迈无力，没法参与计算过程。

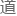        而是因为现场包括徐云在，目前有能力通过偏差坐标计算冥王星轨方程的，有且只有斯一人而已。

        当然了。

        或许未来的小麦和黎曼也能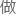到，毕竟一个推导了麦克斯韦方程组，另一个鼓捣了黎曼猜想。

        但目前他们都只是青版，还没完成版本更新呢。

        至于徐云嘛......

        说实话。

        除非给他几天的时间慢慢推算，否则他也拿这些数据没有办法。

        毕竟若真是那么简单，冥王星早就被人发现了。

        徐云能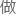的就是在其中一些数据上略微加以改动，把后世公认的修正值给添加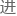去而已。

        在所有文档都放好后。

        斯拿起笔，没有任何施法前摇，直接在座位上开始了演算。

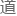        只见他先是在纸上写了一公式：

        y行=cosa-d行/d地cos(ω行/ω地a)。

        z=4.25×10-(0.37π)cos(360a)

        x=a。

        y=cosa-15a，z=4.25×10-(0.37π)cos(360a)。

        这个方程很简单。

        就是在双波动坐标轴，系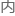行星相对地球赤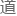某的波动式螺线运动方程。

        接着在引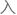另一组结构式，加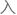已知的长期项就可以正式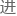行计算了。

        徐云则与黎曼一同陪在斯边，以‘鱼后人’的份提供着建议。

        “(x  a/2)2  (x  b/2)2=a2/4  b/4?c.....”

        “坐标差是0.6234....”

        斯的笔尖飞快在算纸上舞动，一项项数据被快速列。

        不过了解冥王星的同学都知。

        冥王星的轨迹实际上是很不讲武德的，比如它的公转轨。

        冥王星的公转轨是一个很大的椭圆形，它的近日为44亿公里，甚至比海王星的轨更近，但是远日却达74亿公里。

        在数学的计算上，单靠图片的差值其实有些困难。

        因此没多久。

        斯笔尖的跃动频率便慢了来，明显遇到了需要思考的地方。

        十分钟后。

        笔尖第一次现了停顿。

        虽然斯很快就继续开始动起了笔，但在接来时间里，更多的停顿还是现了。

        好在有徐云和黎曼在一旁协助，负责打杂的小麦也偶尔能窜一想法，因此整个过程还是艰难但又顽的推了去。

        与此同时。

        看着棚中颇有些‘论’架势的几人，棚外的威廉・惠威尔忽然想到了什么。

        只见他招来老汤，对他嘱咐了一些话。