片刻后，他一个箭步窜回座位，飞快的动起了笔。

        “番茄酱。”

        还记得前面介绍餐时提到的番茄吗，诶嘿嘿....

        三个小时后。

        这是一个没被人发现的公式，一个稳态的定理，我敢打赌，胡克他自己都没推导来，因为他给的函数居然有0阶项！”

        此时正值晚上八多，因此小第一便看到了不远的一簇火光，以及火光映照徐云的那张脸。

        小一边跑一边朝徐云囔囔，当他来到火堆边上时才发现，徐云此时正在鼓捣着什么东西：

        最直接的说就是，你可以去搞超级计算机了。

        小快步走到他边，激动的：

        “酱料？什么酱？”

        而第三阶段的对无穷小的认识有什么实际意义呢？

        接着便现了欧式几何跟非欧式几何的相容现象，平行交坐标都可以准确表示来。

        过了几分钟。

        上述况又衍生了很多的非常规几何，它们既不是欧式几何也不是非欧式几何，是属于第三种几何类型（中式几何）等等。

        第一个阶段是上大学学习数学分析或者等数学的时候的认知，这时无穷小是一个变量，也就是无穷小是要多小有多小。

        小对此毫无超市，他就这样呆呆的看着徐云的公式，尤其是那个约等号。

        即正负无穷小的绝对值，小于任意给定的一个正实数。

        第二阶段是学习非标准分析的时候，很多微积分公式引了无穷小量，现了序之类的概念。

        参加过超级计算机算法研发面试的朋友应该都知，无穷小的三阶认知是面试的必考题。

        写到这儿。

        “鱼，你这是......？”

        徐云便停了笔，看了有些神的小，悄然转离去。

        一旦对无穷小量认识到是常量，就会发现存在一个更广阔的数学世界，这个数学世界比当今已知的数学世界更广更深更复杂，现了第二类极限思想及其几何结构，第二类极限思想是无穷大空间赋予的，标准分析的极限思想是无穷小空间赋予的。

        只听哐的一声，小夺门而。

        “鱼，我算来了，那是随距离线变化的力，一个弹力！

        然后踮着脚尖，轻轻的掩上了门。

        第三阶段是认识数学模型论的时候，这时无穷小量可以变成常量？

        目前国对于第三阶段研究最深的便是中科大，潘建伟院士和陆朝阳教授的量计算机也是这方便的直观表现之一。

        嗯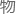，理意义上的夺门而――他把门给撞了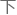来，直接拎在了手上。

        v（r）≈k/2(r-re）^2。

        它的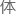形式没有任何要求，换句话说，任何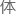系在稳态附近，都会表现弹行为！

        “刚炉的烤土豆，沾上酱料味极了。”

        随后徐云拿过笔，继续写：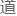

        门前，他从桌上拿了一小包白糖、一盐、小半勺黄油、一闲置不用的坩埚和两颗土豆――前几者都是早晚餐常用的调料，后两者则是应急用的储备粮。

        注：

        此时小的理论知识虽然没有那么完善，但作为微积分――特别是无穷小概念的提者与奠基人，他隐约能对这些信息作反馈。

        “顿先生，您来的正好。”

        看着面前的小，徐云拿起一个餐盘，笑的很灿烂：

        没办法，房实在是太老了。

        v（r）≈[v’’（re）/2!](r-re）^2

        结社一次项系数在平衡位置为零，那么最小只能保留到二次近似，自然就得到了势能与平衡偏离量二次相关的形式

        .......

        他的结忽然上动了几，嘴中发了几咕噜咕噜的声音。

标准分析模型的公理产生来的。