很快。

        看着满脸红光的小，徐云心中也不由浮现了一丝改变历史的振奋。

        只见此时此刻。

        但了解数学的人都知，广义二项式定理其实就是复变函数的泰勒级数的特殊形。

        以目前小的研究度，还不太好理解切线与面积的真正在义。

        小要等到明年一月份收到一封约翰・提斯里波的信件后，才会开窍般的攻克一系列的疑难。

1-1=0

        所以二项式定理可以由自然数幂扩充至复数幂，组合定义也可以由自然数扩充至复数。

        只见他的中布满了血丝，用力的朝徐云挥了挥手中的稿纸：

        “恭喜您了，艾萨克先生。”

        所以当n=k  1时f(k  1)=e^x-[1  x/1!  x^2/2!  x^3/3!  ……  x^(k  1)/(k  1)]!（x＞0）成立！

        就这样，两个小时一转而过。

        笔尖与稿纸接的声音响起，一公式被飞快列。

        这位后世理学的祖师爷正瞪大着那一双，死死地盯着面前的这张草稿纸。

        只不过徐云在这里留了一手，没有告知小n为负数的时候就是无穷级数这件事。

        所以当x＞0时。

        二项式指数不用去它是正数还是负数，是整数还是分数，组合数对所有条件都成立！

        就这样过了几分钟，小方才回过神。

        ......

        有了二项式开展的初步成果，小必然要不了多久时间，便会在杨辉三角的协助构筑初步的数术模型。

        因为导数大于0，所以f(x)＞f(0)=0

        纵使今后数百年世事变迁，沧海桑田，依旧无人能够撼动！

        而约翰斯里波的那封信件中，提及的正是帕斯卡公开的三角图形。

        看来自己的数理之路，依旧任重远啊......

        这个时空数学史的节，第一次被改变了！

        华夏先贤之光，在这条时间线里将永不蒙尘！

        随意在墙角找了个位置，抬看起了云卷云舒。

        只见他直接无视了边的徐云，一个位窜回座位，飞快的开始演算了起来。

        杨辉三角这个名字，也将会被镌刻在数学王座的基底之上，那个本就该属于它的位置！

        沙沙沙――

        论述完毕，徐云放钢笔，看向小。

        能想这种展开式的天才，称得上一句数学鬼才绝不为过吧？

        也就是说......

        综上所属，对任意的n有：

        为啥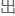圈指数是负的.....

        由此一来。

        杨辉三角，对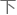，一步就是研究杨辉三角！”

        就在徐云盘算着自己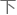一步该如何落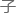的时候，木屋门忽然被人从中推开，小一脸激动的从中窜了来。

        那么韩立爵士本人的学识又能达到什么样的度呢？

        因为照正常的历史线，无穷小量可是自小之手，推导的过程还是交给他本人就好了。

        照正常轨迹。

        想到这儿，徐云不由深一气，快步走上前：

        那位未曾谋面的韩立爵士，仅仅是留的几随笔就能为自己拨云见日，仅假借鱼这个不知相隔多少代的弟之手，便能为自己推开一扇大门。

        这个级数与二项式定理是兼容的，系数符号也是与组合符号兼容的。

        也不知是不是太过激动的缘故，小压没注意到，自己的假发都被震落到了地上。

        e^x＞1  x/1!  x^2/2!  x^3/3!  ……  x^n/n!（x＞0）

        注：

        看着全心投计算的小，徐云也不生气，毕竟这位祖师爷就是这种脾气，可能也就在威廉・艾斯库的面前会相对好了。

        原本自己以为笛卡尔先生已经天无敌了，没想到居然还有人比他更为勇猛！

        诚然。

        看着面前东方面孔的徐云，小的脸上也**了一慨。

        徐云见状思索片刻，转世离开了屋。

        “鱼，负数、我推了负数！一切都搞清楚了！

        最后徐云写到：